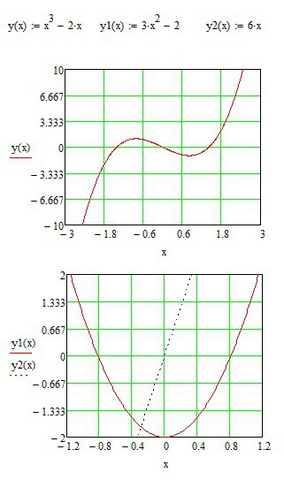
Найдём 1 производную функции y1(x)=3*x^2-2, она равна нулю при х1=-0,816 (производная меняет знак с - на +, точка локального max) и х2=0,816 (производная меняет знак с + на -, точка локального min).
Найдём 2 производную y''(x)=6*x, она равна нулю при x3=0, при положительных х у функции вогнутость, при отрицательных х - выпуклость. Таким образом функция возрастает в интервале от минус бесконечности до х1 и от х2 до плюс бесконечности.
Функция убывает в интервале х1..х2.