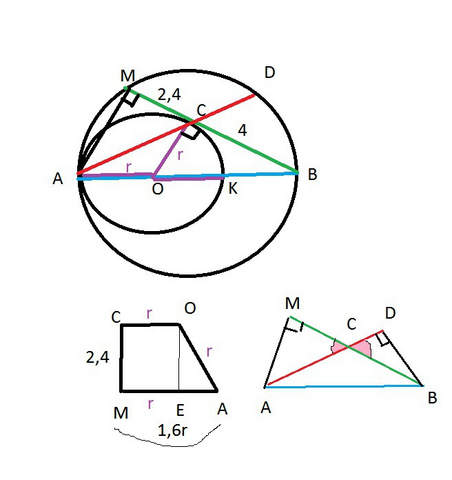
Пусть АО=ОС=r;
Δ CОВ ~ Δ АМВ по двум углам ( ∠В-общий; ∠АМВ=∠ОСВ).
СО:АМ=СВ:МВ;
r: AM=4:6,4⇒ AM=1,6r
Рассмотрим прямоугольную трапецию МСОА. Проведем высоту СЕ.
(см чертеж 2, отдельный)
Из прямоугольного треугольника ОЕА по теореме Пифагора
ОА²=ОЕ²+ЕА²;
r²=2,4²+0,36r²;
0,64r²=5,76
r²=9
r=3.
АМ=1,6r=1,6·3=4,8
Из прямоугольного треугольника АМС по теореме Пифагора
АС²=АМ²+МС²;
АС²=4,8²+2,4²=(2,4·2)²+2,4²=2,4²·(2²+1)=2,4²·5
АС=2,4√5
Δ AMC ~ Δ CMD
AC : BC=MC : CD;
2,4√5 : 4=4,8 : СD ⇒ CD=8√5/5=1,6√5
AD=AC+CD=2,4√5+1,6√5=4√5.
По свойству касательной и секущей, проведенных к окружности малого радиуса из точки В:
произведение секущей ВА на ее внешнюю часть ВК равно квадрату касательной ВС
ВА· (ВА-AK)=BC²; AK=2r=2·3=6
ВА· (ВА-6)=4²;
ВА²-6ВА-16=0- квадратное уравнение.
D=36+64=100
BA=(6+10)/2=8
BA=2R
2R=8
R=4
О т в е т. R=4; r=3; AD=4√5