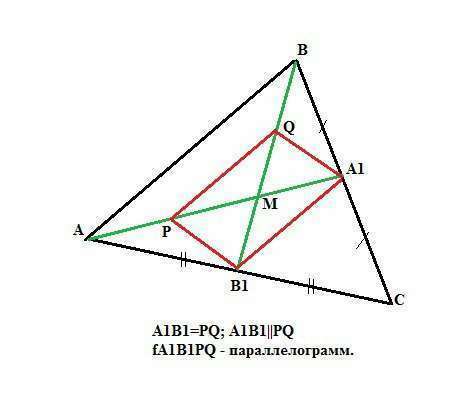
Если имеется в виду:"В треугольнике ABC проведены медианы AA1 и BB1, которые пересекаются в точке M, а в треугольнике AMB проведена средняя линяя PQ, параллельная AB. Докажите что A1B1PQ - параллелограмм", то решение такое:
A1B1 - средняя линия треугольника ABC, параллельная стороне AB, так как AB1=B1C и BA1=A1C (поскольку AA1 и BB1 - медианы).
Значит А1В1=0,5*АВ.
PQ - средняя линия треугольника АВМ, параллельная стороне АВ (дано), значит PQ=0,5*АВ.
Если А1В1 параллельна АВ и PQ параллельна АВ, то А1В1 параллельна PQ.
Тогда четырехугольник А1В1PQ - параллелограмм по признаку: "Противоположные стороны равны и параллельны": A1B1=PQ; A1B1||PQ".
Что и требовалось доказать.