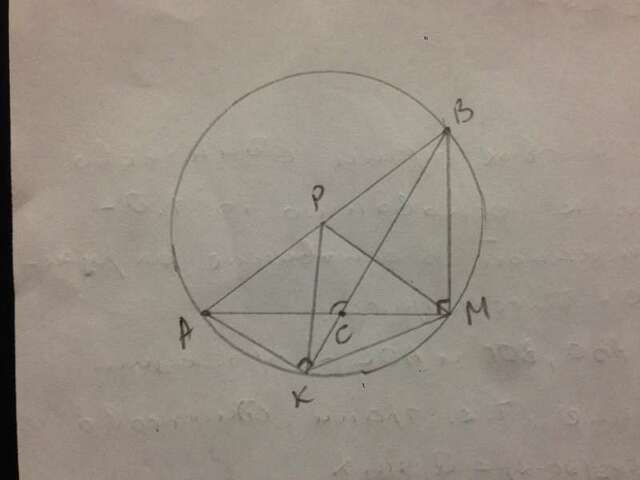
Треугольники АВК и АВМ прямоугольные, опирающиеся на общую гипотенузу, значит оба они вписаны в одну окружность. Радиус окружности R=АР=ВР=КР=МР=АВ,2=16/2=8.
Если точка пересечения двух секущих к окружности находится внутри окружности, то угол между секущими равен полусумме дуг, которые они высекают. АМ и ВК - секущие, значит ∠АСВ=(∩АВ+∩КМ)/2 ⇒ ∩КМ=2·∠АСВ-∩АВ=2·105°-180°=30°, следовательно ∠KРМ=30°.
Площадь тр-ка МКР: S=КР·МР·sin30°/2=8·8/4=16 (ед²) - это ответ.