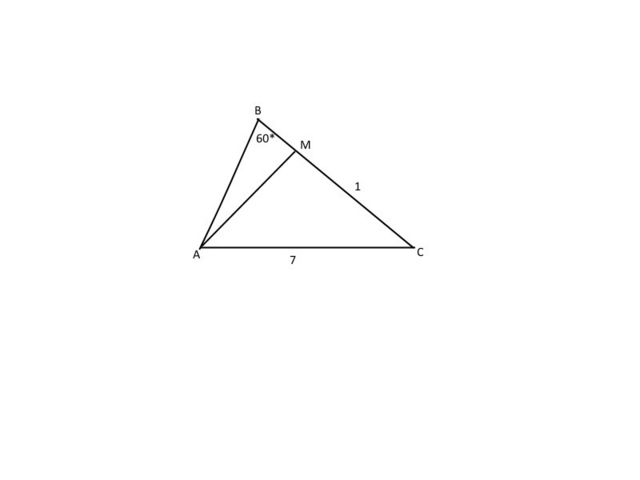
1)Найдём высоту АМ
Из ΔАМС(∠АМС=90°)
По теореме Пифагора
АС²=АМ²+МС²
7²=АМ²+1
АМ²=49-1
АМ²=48
АМ=√48=4√3
2)Из ΔАВМ
∠ВАМ=90°-∠АВМ=90°-60°=30°
Так как катет ВМ лежит против ∠ВАМ=30°, то он равен половине гипотенузы АВ. АВ=2ВМ
Рассмотрим прямоугольный ΔАВМ(∠ВМА=90°)
Пусть ВМ=х, тогда АВ=2х
По теореме Пифагора
АВ²=ВМ²+АМ²
(2х)²=х²+(4√3)²
4х²=х²+48
3х²=48
х²=16
х=4
АВ=2х=2*4=8 см
Ответ 8см