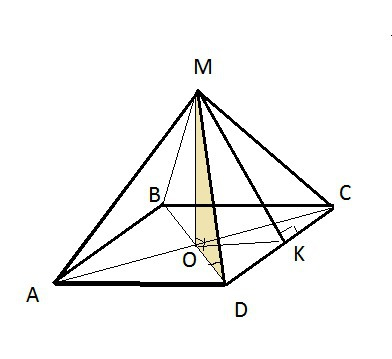
В основании пирамиды квадрат АВСD.
Пусть сторона квадрата равна х.
Диагонали квадрата равны и в точке пересечения делятся пополам.
АС=BD=x√2 - диагонали квадрата.
ОD=(1/2)BD=x√2/2.
Из прямоугольного треугольника МОD:
MO=OD·tgα=(x·√2·tgα)/2
MD=OD/cosα=(x√2)/(2cosα)
По теореме Пифагора из прямоугольного треугольника МDK:
MD²=DK²+MK²
(2x²)/(4cos²α)=(x/2)²+a² ⇒ x²·(2-cos²α)/4cos²α=a² ⇒
x=2acosα/√(2-cos²α)
V ( пирамиды)=(1/3)·S( осн.)·H=(1/3)·x²·(x·√2·tgα)/2=
= (8a³cos³α·tgα)/(3·(2-cos²α)·√(2·(2-cos²α))).