Из прямоугольной трапеции с основаниями a и b и высотой h вырезают прямоугольник...

Question

Из прямоугольной трапеции с основаниями a и b и высотой h вырезают прямоугольник наибольшей площади. Чему равна эта площадь,если:

а) a=80, b=60,h =100

В решебнике решено,но не понятно откуда взято,что "tg a=5 " и с чего взяли что х принадлежит (0:100). Кто понимает,обьясните. Фотография во вложениях

---

Answer 1

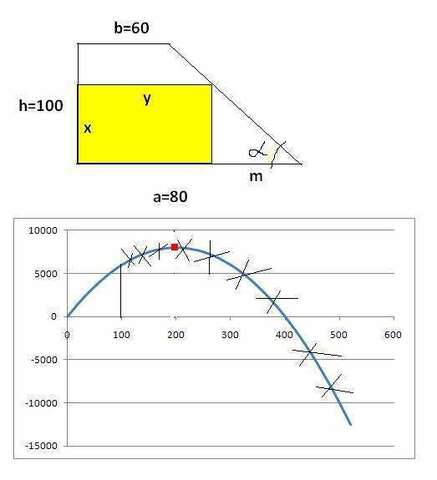
Смотрите рисунок во вложении
tan(альфа)=h/(a-b)=100/20=5
tan(альфа)=x/m
подставляем вместо тангенса 5 из первого уравнения, а m=80-y, тоже подставляем.
5=x/(80-y) из этого выражаем у через  x
y=80-x/5

Площадь прямоугольника S=x*y=х*(80-x/5)=80х-x^2/5
Берем производную функции площади по х.
S'=80-2x/5
Для нахождения максимума приравниваем производную к нулю и ищем х
80-2x/5=0
2x/5=80
2x=400
x=200
Если бы мы построили график функции площади, смотри на рисунке, то у него бы была лишь одна точка максимума, там,где х=200, до этого значения он бы возрастал, а после него убывал.
Но посмотрите еще раз на рисунок. Х не может быть больше высоты трапеции, то есть больше ста. Поэтому фунцию после значения в точке 100 можно смело вычеркивать, ее там просто нет.
при Х=100 У=60
Ответ S=6000

Так понятнее?

---