Основою піраміди є правильний трикутник. Радіус кола, вписаного в основу, дорівнює 3 см....

Радиус вписанной окружности OE

$r=\frac{\sqrt3}6AB\\ AB=r\cdot\frac6{\sqrt3}=\frac6{\sqrt3}\cdot3=6\sqrt3$

Радиус описнной окружности OF

$R=\frac{\sqrt3}3\cdot AB=\frac{\sqrt3}3\cdot6\sqrt3=6$

Площадь ABC

$S_{ABC}=3\sqrt3\cdot r^2=3\sqrt3\cdot9=27\sqrt3$

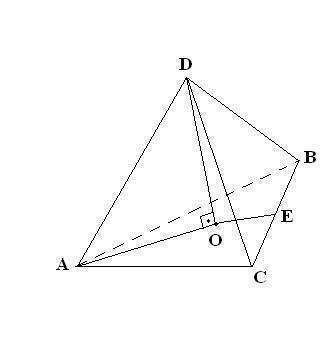
Опустим высоту пирамиды DO из вешины D на основание ABC.

Пирамиды правильная, значит высота опустится в центр треугольника ABC . Точка O совпадёт с цетрами вписанной и описанной окружностей.

Рассмотрим треугольник ADO. Он прямоугольный (DO перпендикулярно AO).

По определению тангенса

$tg(\widehat{DAO})=\frac{DO}{AO}\\ DO=tg(\widehat{DAO})\cdot AO=tg30^o\cdot6=\frac1{\sqrt3}\cdot6=2\sqrt3$

Тогда объём пирамиды

$V=\frac13Sh=\frac13S\cdot DO=\frac13\cdot27\sqrt3\cdot2\sqrt3=18\cdot3=54$