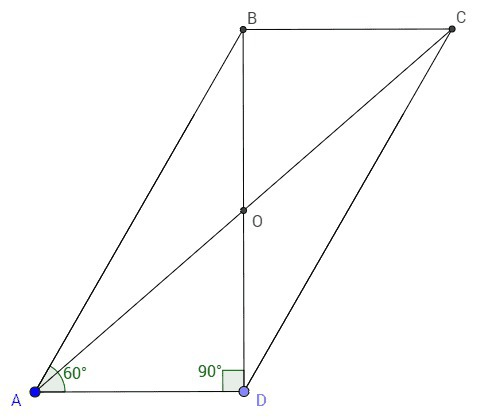
Сумма углов параллелограмма прилегающих к любой стороне равна 180°
∠DAB+∠CDA =180°
∠CDA= 180°-60° =120°
∠BDA= 120°·3/4 =90°
Высота равностороннего треугольника: h= (√3/2)a
BD= AB·√3/2 <=> AB= BD·2/√3
AB= 8√3·2/√3 =16
Сумма углов треугольника равна 180°
∠ABD= 180°-60°-90° =30°
Катет, лежащий против угла 30°, равен половине гипотенузы.
AD= AB/2
AD= 16/2 =8
P= 2(AB+AD)
P= 2(16+8) =48
Диагонали параллелограмма точкой пересечения делятся пополам.
OD= BD/2
OD= 8√3/2 =4√3
AO= √(AD^2 + OD^2)
AO= √(64 + 3·16) =√112 =4√7
AC= 2AO
AC= 2·4√7 =8√7 (~21.17)