При пересечении двух плоскостей образовался угол, равный 45 град. Расстояние от точки А,...

Question

При пересечении двух плоскостей образовался угол, равный 45 град. Расстояние от точки А, принадлежащей одной из плоскостей , до другой плоскости равно d. Найдите расстояние от этой точки до прямой пересечения этих плоскостей.

Answer 1

 

размер линейного угла между плоскостями  = 45 град 

расстояние от точки А до линии пересечения плоскостей - это гипотенуза - с

расстояние от точки А до её прекции на  вторую плоскость - это катет - a=d

проекция гипотенузы  на  вторую плоскость - это  второй катет  - b= d

получается  равнобедренный прямоугольный треугольник с углами при основании 45 град

по теореме Пифагора  c^2 = a^2 +b^2

оба катета  =d

c =  d√2

Answer 2

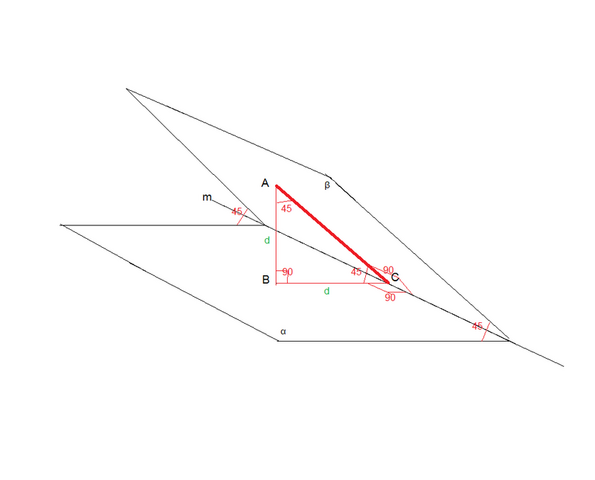
Сделаем построение по условию.

 

Обозначим  плоскости α , β.

Прямая    m – линия пресечения плоскостей.

По условию т.А принадлежит плоскости β  ,  |AB| ┴   α , |AB|=d

Расстояние от  точки А  до прямой   m отрезок |AC| ┴ m .

Точка  В – проекция точки А.

Расстояние от  точки B  до прямой   m отрезок |BC| ┴ m .

По теореме о трех перпендикулярах точки А,В,С лежат в одной плоскости и образуют

прямоугольный треугольник . 

Так как по условию  <( α , β) =45 град, следовательно  <ACB =45 град.</p>

Значит 

Треугольник   ∆ABC  - прямоугольный, равнобедренный.  |BC|=|AB|=d

По теореме Пифагора  искомое расстояние  AC^2  = AB^2 +BC^2 =2d ;  AC=d√2

 

ОТВЕТ  d√2

---