Решение 1. Существует формула для определения радиуса вписанной окружности по площади фигуры, в которую она вписана, и по полупериметру этой фигуры.
r=S/p
S=ab/2 для прямоугольного треугольника
p=(a+b+c)/2 для произвольного треугольника
r=ab/2 / ((a+b+c)/2)=ab/(a+b+c)
2r=2ab/(a+b+c)
Допустим, исходное выражение верно. Тогда 2ab/(a+b+c)=a+b-c должно быть тождеством для a,b,c, являющихся сторонами прямоугольного треугольника.
2ab=(a+b+c)(a+b-c)
2ab=(a+b)^2-c^2
2ab=a^2+2ab+b^2-c^2
a^2+b^2=c^2
Действительно, получилось верное равенство для прямоугольного треугольника. Значит, утверждение 2r=a+b-c верно для прямоугольного треугольника.
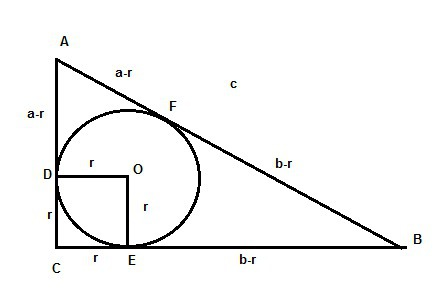
Решение 2. Изобразим прямоугольный треугольник на рисунке. O - центр вписанной окружности, D, E, F - точки касания окружности сторон AC, BC и AC соответственно. Ввиду того, что угол C прямой, OD⊥AC, OE⊥BC, четырехугольник ODCE является квадратом. Это значит, что CD=ED=r. Если AC=a, BC=b, AC=c, то AD=a-r=AF, BE=b-r=BF. Отсюда следует, что AF+BF=a-r+b-r=c. То есть 2r=a+b-c, что и требовалось доказать.