1.
Квадратное неравенство.
Замена переменной
sinx=z
5z²>11z+12;
5z²-11z-12>0
D=(-11)²-4·5·(-12)=121+240=361=19²
z=(11-19)/10=-4/5 или z=3
Решаем неравенство методом интервалов:
____(-4/5)_______(3)____
\\\\\\\\\ /////////
z<-4/5 или z>3
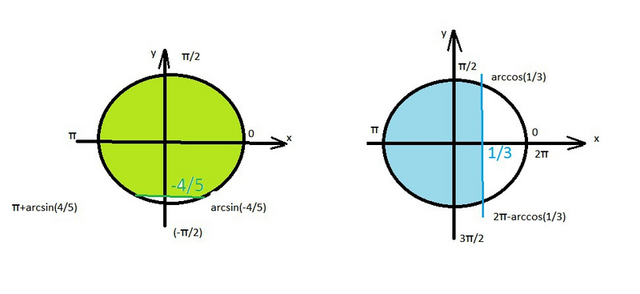
sint<-4/5 или sint>3 - неравенство не имеет решений.
arcsin(-4/5)+2πk < t < π+arcsin(4/5)+2πk, k∈Z.
О т в е т. -arcsin(4/5)+2πk < t < π+arcsin(4/5)+2πk, k∈Z.
2.
cos4x < 1/3
arccos(1/3)+2πn< 4x <2π-arccos(1/3)+2πn, n∈Z;<br>(1/4)·arccos(1/3)+2πn < x < (π/2)-(1/4)·arccos(1/3)+2πn, n∈Z.
О т в е т.(1/4)·arccos(1/3)+2πn < x < (π/2)-(1/4)·arccos(1/3)+2πn, n∈Z.