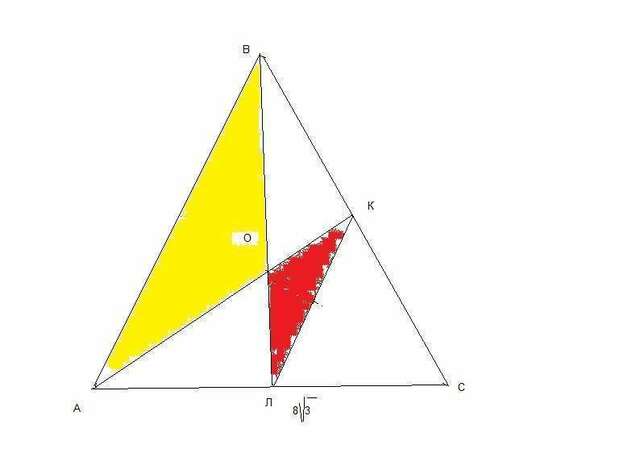
Смотри рисунок.
не будем говорить про банальные вещи - у равностороннего треугольника все стороны равны, все углы =60, медианы , биссектрисы и высоты являются одними и теми же линиями и пересекаются в одной точке.
Просто вспомним
1) нахождение площади треугольника = половина произведения сторон на синус угла между ними. В данном случае - стороны равны, угол =60
2) то, что ЛК естественно, средняя линия и равна половине АВ (Л и К -середины соответствующих сторон)
3) то, что площадь АВО равна трети исходного ( все три треугольника, составляющих исходный, равны по ... (например, по трем сторонам - т.к. основания равны, а стороны являются радиусами описанной окружности)
4) площади подобных треугольников пропорциональны квадрату коэфф.
подобия ( основания в данном случае различаются в 2 раза , значит и высоты тоже в 2, площадь в 2*2=4 раза)
а теперь решение
8√3*8√3*sin60 /2(площадь исходного) / 3 (площадь желтого) /2² = 4√3
все.