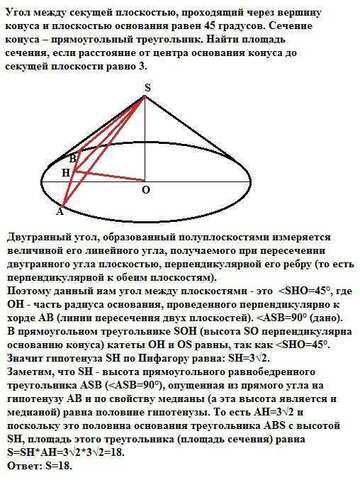
Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям).
Поэтому данный нам угол между плоскостями - это В прямоугольном треугольнике SOH (высота SO перпендикулярна основанию конуса) катеты ОН и ОS равны, так как Заметим, что SH - высота прямоугольного равнобедренного треугольника АSВ (гипотенузу АВ и по свойству медианы (а эта высота является и медианой) равна половине гипотенузы. То есть АН=3√2 и поскольку это половина основания треугольника ABS с высотой SH, площадь этого треугольника (площадь сечения) равна S=SH*AH=3√2*3√2=18.
Ответ: S=18.