Формула площади боковой поверхности конуса
S=π r l
где r-радиус его основания, - l-образующая.
Радиус и образующую предстоит найти.
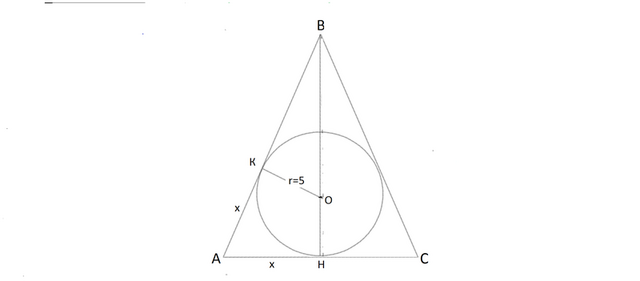
Сделаем рисунок осевого сечения конуса и шара, вписанного в него.
Это сечение - равнобедренный треугольник с вписанной в него окружностью.
Рассмотрим прямоугольный треугольник ВКО.
ВО = высота без радиуса
ВО=18-5=13
Тогда ВК, как сторона треугольника с отношением Пифагоровой тройки равна 12
( можно проверить т. Пифагора, получится такая же длина ВК)
В треугольнике АВН отрезок АК=АН как части касательных к окружности.
Пусть они равны х.
Тогда АВ=12+х.
АВ²=ВН²+АН²
(12+х)²=18²+х²
144+24х+х²=324+х²
24х=180
х=7,5
Радиусоснования конуса равен 7,5
Образующаяравна 12+7,5=19,5
S=π r l=π*7,5*19,5=146,25π или ≈ 459,458