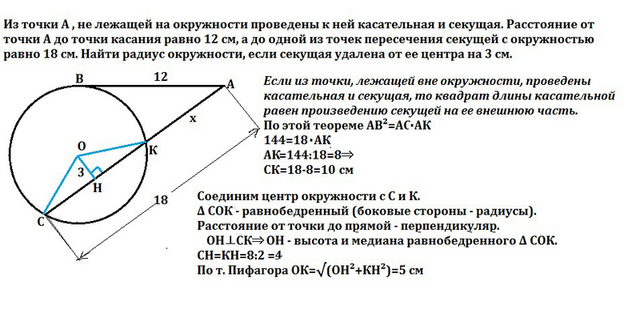
Пусть точка касания будет В, секущая АС, ближняя к А точка её пересечения с окружностью К.
Если из точки, лежащей вне окружности, проведены касательная и
секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть.
По этой теореме АВ²=АС:АК
144=18*АК
АК=144:18=8⇒
СК=18 - 8=10
Соединим центр окружности с С и К.
∆ СОК - равнобедренный (боковые стороны - радиусы).
Расстояние от точки до прямой - перпендикуляр.
ОН⊥СК⇒ ОН - высота и медиана равнобедренного ∆ СОК.
СН=КН=8:2=4
По т. Пифагора ОК=√(ОН²+КН²)=5 см