Собственно, вот в этой задаче (znanija.com/task/2360115) я уже решал, но почему-то пропали прикреплённые картинки. По этой причине повторюсь.
Если принять сторону основания за a, a ребро за b, то в зависимости от расчёта приходим к одной из формул (они приводимы друг к другу):


Сначала доказываете, что плоскость BMD перпендикулярна AC, далее - перпендикулярна A'C', A'C' пересекает BMD в точке P, ну и перпендикулярна всем прямым данной плоскости, проходящим через P => ND перпендикулярна A'C'.
Т.о. 
т.е. 
Найдём длины нужных нам в дальнейшем отрезков:



В треугольнике BMD DM и MO это медианы, пересекающиеся в точке P. Т.о. 
AC || A'C' из подобия треугольников AMC и A'MC' следует, что 
т.е. 






Теперь подставляем значения в формулу:


Ответ: 
P.S.> Для примера - есть вариант, где a=6, b=12. В этом случае результат будет следующий:


Это соответствует правильному ответу.
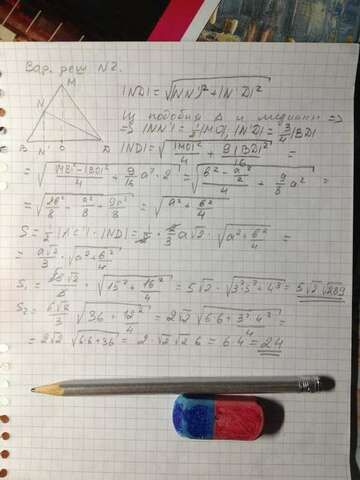
P.P.S.> Попробую прикрепить ещё снимки решения на бумаге (если получится) - там 2 варианта. Почему-то не всегда прикреплённые картинки сохраняются. По этому и вбил решение текстом.