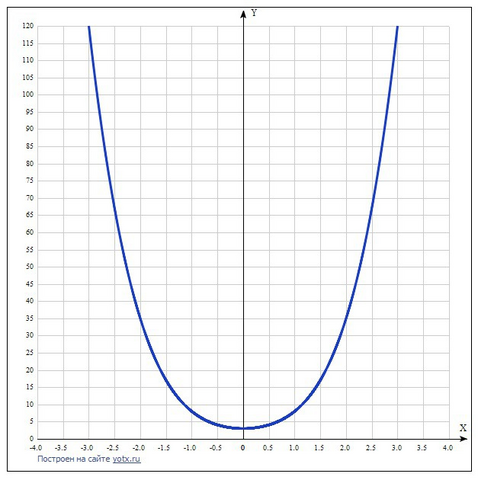
Производная функции: y = x^4 +4x^2 +3 равна:
y' = 4x³ + 8x = 4х(х² + 2).
Приравняем её нулю:
4х(х² + 2) = 0.
Имеем только 1 корень (точку экстремума функции): х = 0.
Исследуем знаки производной вблизи найденной критической точки:
х = -0.5 0 0.5
y'=4x^3+8x
-4.5
0 4.5 .
Производная меняет знак с - на + это минимум функции.
График симметричен относительно оси Оу, функция чётная.
При -∞ < x < 0 функция убывает (производная отрицательна),
при 0 < x < ∞ функция возрастает (производная положительна).<hr>