Тут все дело в свойствах логарифмов.
1) Число под логарифмом должно быть положительно: x > 0
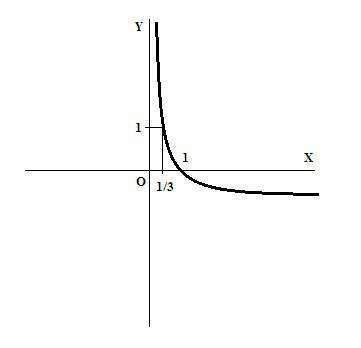
2) Логарифм по основанию 1/3 - убывающая функция, ее график примерно показан на рисунке.
а) 1 = log_(1/3) (1/3) (логарифм по осн. 1/3 от того же 1/3)
log_(1/3) x > 1
log_(1/3) x > log_(1/3) (1/3)
Так как функция убывающая, то при переходе от логарифмов к числам знак неравенства меняется.
x < 1/3
Но мы знаем, что x > 0. Поэтому
0 < x < 1/3
а - 1
б) -1 = log_(1/3) (3) (логарифм по осн. 1/3 от 3)
log_(1/3) x < -1
log_(1/3) x < log_(1/3) (3)
x > 3
б - 4
в) log_(1/3) x > -1
log_(1/3) x > log_(1/3) (3)
x < 3
Но мы знаем, что x > 0. Поэтому
0 < x < 3
в - 2
г) log_(1/3) x < 1
log_(1/3) x < log_(1/3) (1/3)
x > 1/3
г - 3