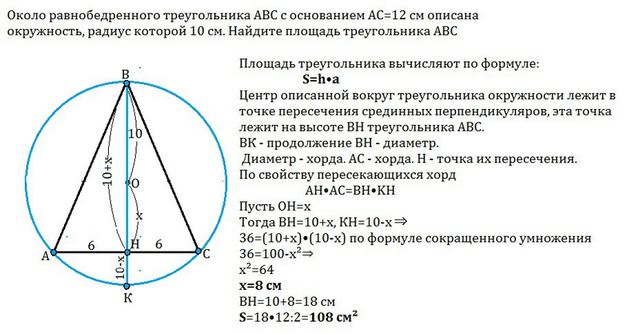
Площадь треугольника равна половине произведения длины высоты на длину основания, к которому она проведена.
S=h•a
Центр описанной вокруг треугольника окружности лежит в точке пересечения срединных перпендикуляров, эта точка лежит на высоте ВН треугольника АВС.
ВК - продолжение ВН - диаметр, Диаметр - хорда. АС - хорда. Н - точка их пересечения. По свойству пересекающихся хорд
АН•AC=BH•KH
Пусть ОН=х
Тогда ВН=10+х, КН=10-х ⇒
36=(10+х)•(10-x) по формуле сокращенного умножения
36=100-х²⇒
х²=64
х=8 см
ВН=10+8=18 см
S=18•12:2=108 см²