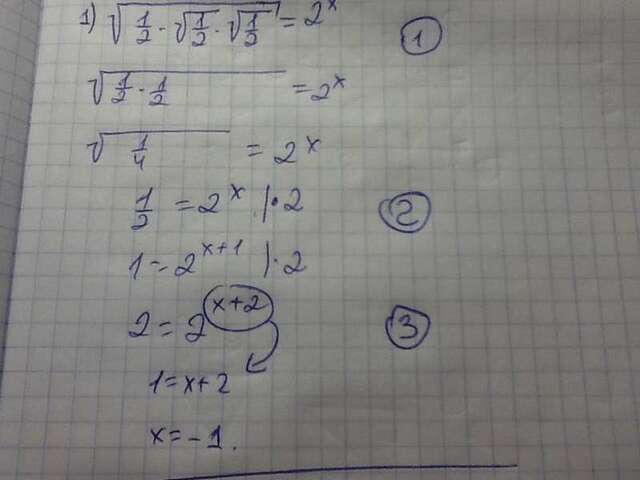(1) - корень, умноженный на корень, объединяем в один большой корень из (1/2*1/2)=корень из (1/4)= 1/2.
(2) - домножаем на 2, чтобы убрать дробь. Получается в правой части 2^х*2=2^(х+1) (так как ещё одна двойка).
Домножаем ещё раз на 2, чтобы уравнять главные числа. 2=2. (3) Следовательно, показатели степеней тоже равны. В левой части показатель 1, в правой (х+2). х=-1.
2. Разделим на 2 части. Решаем первую часть. Представим, что под знаком корня формула квадрата разности, просто сложённая.
1* Тогда 71-16√7=а²-2ав+в².
Разделяем. 16√7=2ав.
Делим обе части на 2. 8√7=ав.
Какие числа нужно умножить, чтобы получить 8√7? (2) 4*2√7=8*√7=2*4√7. Пока оставим так.
Из 1* следует, что 71=а+в. Метод подбора. Что из (2) нам подойдёт? 8*√7. 71=64+7=71. Подсоединяем.
√(8-√7)²=8-√7.
Тем же методом разбираемся со второй частью. 2ав=4√7. ав=2√7=2*√7.
а²+в²=11.
Соединяем. √(2-√7)²=|2-√7|= √7-2.
2 БОЛЬШИЕ части объединяем. 8-√7+√7-2=6.
Спасибо за указание ошибки.