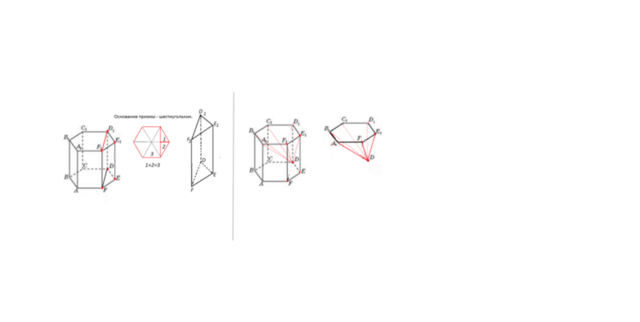
Решение задачи сводится к правильному рисунку,
из которого будет ясно, что многогранник, объем котороно следует найти -
трехгранная призма, в основании которой тупоугольный треугольникD₁E₁F₁ , состоящий из 2-х половинок правильного треугольника.
Площадь основания этой призмы равна 1/6 площади основания исходной, в основании которой - правильный шестиугольник.
А он, как известно, состоит из 6 равносторонних треугольников.
Следовательно, объем этой "вписанной" призмы составляет 1/6 объема исходной:
V=Sh:6=8·9:6=12
--------------------------------
Размеры призмы из задачи, данной во вложении - иные, и многогранник, объем которого следует найти - правильная шестигранная пирамида, но принцип решения тот же.
V пирам. =Sh:3
Высотой пирамиды здесь будет ребро призмы DD1, т.е высота призмы, и площадь основания пирамиды равна площади основания призмы.
Объем многогранника будет равен 1/3 объема исходной призмы:
V=Sh:6=12·2:3= 8