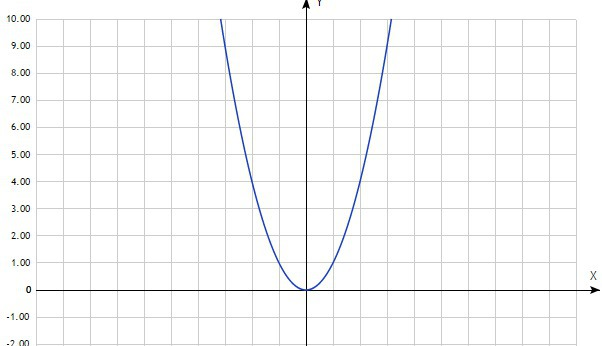
Y=x² - парабола, ветви которой направлены вверх, а вершина в точке с координатами (0;0). Эта же точка и будет наименьшим значением функции.
Если вы изучали производные, то надо найти значение функции в критических точках, для этого находят производную функции и приравнивают её к 0
y'=(x²)'=2x=0
x=0
Подставляем значение х в функцию и находим
y=0²=0
Больше критических точек нет, поэтому дальше находим значение функции на концах отрезка:
y=(-3)²=9
y=2²=4
Теперь сравниваем полученные значения и определяем наибольшее и наименьшее.
Ответ: наибольшее значение функции на отрезке [-3;2] 9, а наименьшее - 0