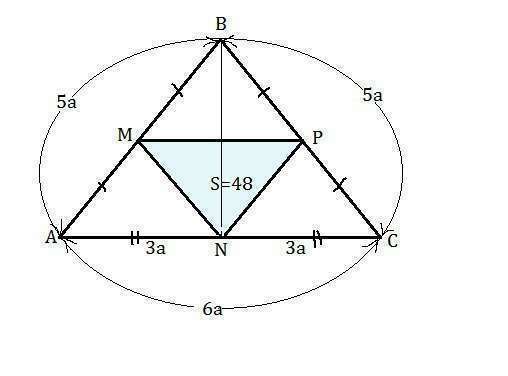
МР=АС:2, MN=BC:2, PN=AB:2, МР, PN и MN- средние линии ∆ АВС. ⇒
∆ ВМР и ∆ АВС подобны ( легко докажете сами)
Коэффициент подобия k=1/2
Площади подобных треугольников относятся как квадрат коэффициента подобия.
S1:S=k²=1/4
Тогда S∆ ABC=48*4=192
Пусть коэффициент отношения сторон ∆АВС будет а.
Тогда АВ=ВС=5а, АС=6а
Опустим из В высоту на АС. В равнобедренном треугольнике высота еще и медиана и биссектриса, ⇒АN=CN=3a.
Найдем по т.Пифагора высоту:
BN=√(AB²-AN²)=√16a²=4a
По формуле площади треугольника
S ∆ ABC=4a*6a:2=12a²
12a²=192
a²=16
a=√16=4
P=5а+5а+6а=16а
Р=16*4=64
-------
Можно площадь ∆ АВС найти несколько иначе:
МР, PN и MN- средние линии ∆ АВС. Они делят ∆ АВС на 4 равных треугольника. : S ∆ ABC=48*4=192