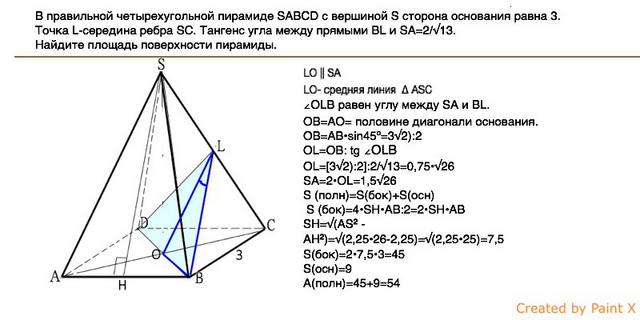
В правильной четырехугольной пирамиде SABCD с вершиной S сторона основания равна 3. Точка L-середина ребра SC. Тангенс угла между прямыми BL и SA=2/√13.
Найдите площадь поверхности пирамиды.
Прямые SA и BL лежат в разных плоскостях, - они скрещивающиеся. Угол между ними - это угол межд BL и пересекающейся с ней прямой, лежащей в той же плоскости и параллельной прямой SA.
L - середина SC, центр основания О - середина АС, ⇒ OL - средняя линия ∆ ASC и равна половине АS.
OL лежит в плоскости ∆ BLD и плоскости ASC и как средняя линия ∆ ASC параллельна AS.
∠OLB равен углу между SA и BL.
ОВ=АО= половине диагонали основания.
ОВ=АВ•sin45º=3√2):2
OL=OB: tg ∠OLB
OL=[3√2):2]:2/√13=0,75•√26
SA=2•OL=1,5√26
S (полн)=S(бок)+S(осн)
S (бок)=4•SH•AB:2=2•SH•AB
SH=√(AS² -AH²)=√(2,25•26-2,25)=√(2,25•25)=7,5
S(бок)=2•7,5•3=45
S(осн)=9
S(полн)=45+9=54