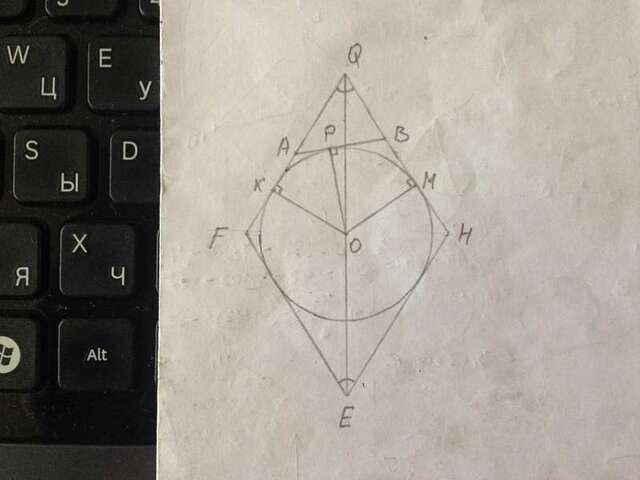
В ромбе ЕFQН ∠Е=∠Q=α. S(QАВ)=S. ОК=ОР=ОМ=r.
В тр-ке QOК QK=OK/tg(α/2)=r/tg(α/2).
Четырёхугольник QМОК - дельтоид в котором две пара смежных сторон равны и пара противолежащих углов прямые.
S(QМОК)=QK·OK=r²/tg(α/2).
Пусть АК=х, ВМ=у.
Касательные к окружности из одной точки равны, значит АК=АР=x и ВМ=ВР=y.
Аналогично S(КАРО)=АК·ОК=rx, S(РВМО)=ВМ·ОМ=ry.
S(QМОК)=S(QAB)+S(КАРО)+S(РВМО),
r²/tg(α/2)=S+rx+ry,
r²/tg(α/2)-S=r(x+y),
x+y=r/tg(α/2)-S/r.
АВ=АР+ВР=х+у.
 - это ответ.
- это ответ.