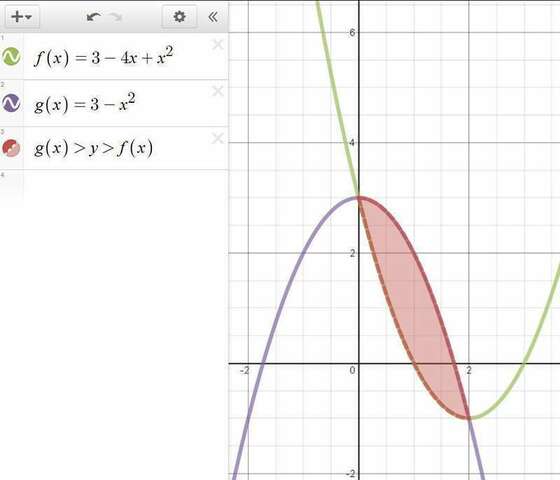
Графически это выглядит следующим образом (см. вложение). Нам нужна площадь области, выделенной красным цветом (честно говоря, полчаса соображал, как это сделать в программе, чтобы она меня поняла)).
Алгоритм такой:
0. Обе параболы поднимаются на 1 единицу вверх, чтобы мы могли вычислить определённый интеграл (он ограничен осью x). Площадь фигуры при этом не изменится, так что всё нормально.
1. Вычисляется площадь фигуры под

;
2. Теперь — под

;
3. Разность площадей

и будет искомой фигурой.
По дороге ещё придётся найти нули функции, т. к. для определённого интеграла нужна область вычисления.
Поехали.
1)

2)

3)

(кв. ед.)
Вроде бы так... :)
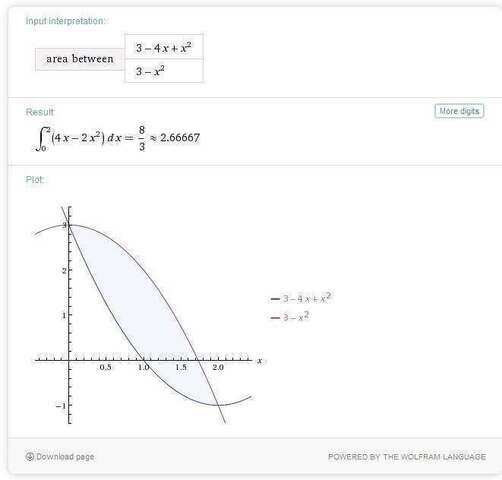
Попробую сейчас проверить решение.
upd: да, всё сошлось.