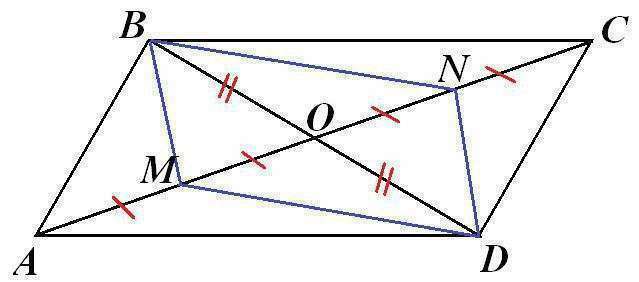
Пусть АС и BD - диагонали параллелограмма АВСD, которые пересекаются в точке О. По условию АМ=МО и ON=NC.
Т.к. диагонали параллелограмма точкой пересечения делятся пополам, то АМ=МО=ON=NC.
Рассмотрим четырехугольник MBND. BD и MN - его диагонали, О - точка их пересечения. По доказанному ВО=ОD и MO=ON. Значит, в четырехугольнике MBND диагонали, пересекаясь, точкой пересечения делятся пополам, поэтому MBND — параллелограмм.
В параллелограмме противоположные противоположные углы равны. А это и есть требуемое равенство, т.е. ∠MBN = ∠MDN.
Доказано.