В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины...

Question

В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 32 градуса. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах

Answer 1

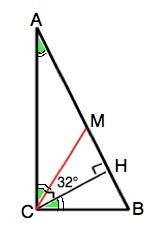
Медиана прямоугольного треугольника, проведенная из прямого угла, равна половине гипотенузы и делит треугольник на два равнобедренных. 

В ∆ АМС ∠САМ=∠МАС, 

Высота, проведенная из прямого угла, делит прямоугольный треугольник на подобные. ⇒∠НСВ=∠НАС=МАС. 

∠АСВ=угол АСМ+угол МСН+угол НСВ. 

Так как углы САМ и НСВ равны, то 

2 ∠САМ+32°=90°

∠САМ=(90°-32°):2=58°:2=29°

Сумма острых углов прямоугольного треугольника равна 90° ⇒

∠АВС=90°-29°=61°

---

Comments

Спасибо. Но уже 1 год и 1.5 месяца, как мне это не нужно)

---

Это понятно. Но задача осталась без решения, она пользуется спросом. Поэтому ответы на популярные вопросы всё же нужно давать. И они, по возможности, даются.