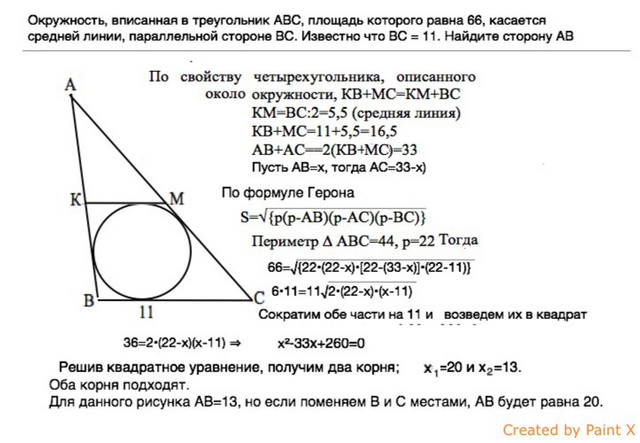
Окружность, вписанная в треугольник ABC, площадь которого равна 66, касается средней линии, параллельной стороне BC.
Известно что BC = 11. Найдите сторону AB
–––––––––––
Обозначим среднюю линию КМ.
По свойству средней линии
КМ=ВС
:2=11
:2=
5,5
ВКМС - описанный вокруг окружности четырехугольник.
Суммы противоположных сторон описанного четырехугольника равны ( свойство). ⇒
КВ+МС=КМ+ВС
КВ+МС=5
,5+11=16,5
К и М делят АВ и АС пополам, ⇒
АВ=2₽•KB
АC-2•MC
АВ+АС=2•(КВ+МС)=
33
Пусть АВ=х, тогда АС=33-х
Периметр ∆ АВС=АВ+АС+ВС=33+11=44
Формула Герона для вычисления площади треугольника:
–––––––––––––––––
S=√[р(р-АВ)(р-АС)(р-ВС)] где р - полупериметр
р=44
:2=22⇒
––––––––––––––––––––––
66=√[22•(22-х){22-(33-x)}(22-11) Выведем из-под корня 11:
6•11=11√[2•(22-x)(x-11)]
Сократим обе части на 11 и возведем их в квадрат:
36=2•(22-х)•(x-11) ⇒
x²-33 x+260=0
Решив квадратное уравнение, получим два корня: х₁=20; х₂=13.
Оба коря подходят.
Для данного в приложении рисунка АВ=13 ( а АС=20). Если поменять местами В и С, АВ будет равно 20.