Я пытался вам проилюстрировать ответы. См. вложения.
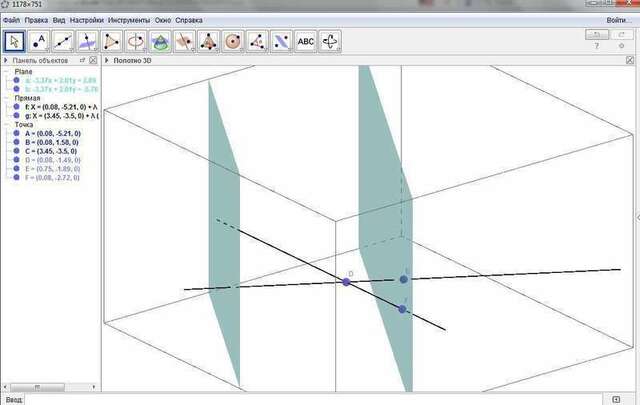
1) Неверно: через две прямые может проходить как ни одной плоскости, так и бесконечное их множество (см. рис. 1)
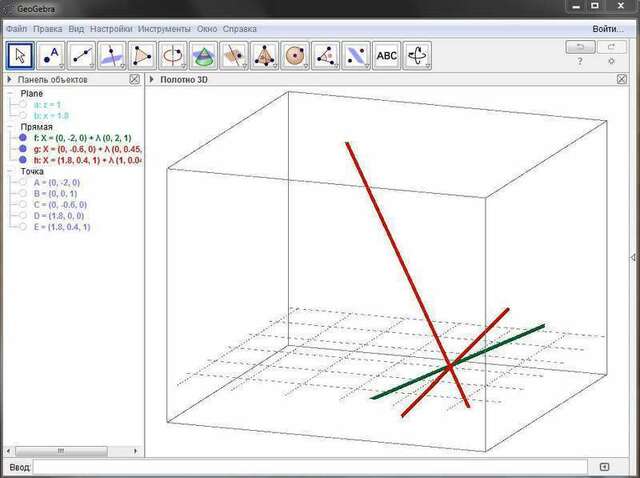
2) Неверно, см. рис. 2: обе красные прямые перпендикулярны зелёной, но не параллельны друг другу, потому что одна перпендикулярна по оси 
, а другая — по оси 
.
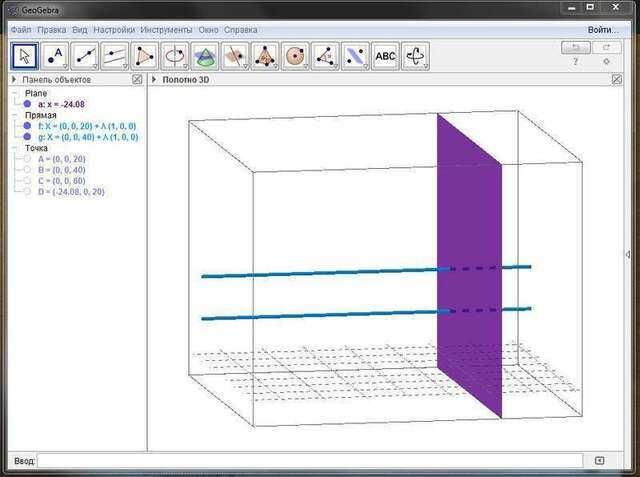
3) Верно: если одна прямая пересекает плоскость, то и другая не может не пересекать. Возможен другой вариант: плоскость параллельна одной из прямых, поэтому другую не пересекает, но тогда первая прямая будет не пересекать плоскость, а полностью лежать в ней, а это совсем другое.
Поэтому правильный ответ — 3.
Сейчас сделаю второе задание.
UPD: второе задание. Я не помню, как оно правильно и индуктивно решается :) Поэтому как есть, но ответ точно правильный. Все возможные комбинации: ooo, ppp, opp, oop. Нам нужна комбинация «оор» (орёл-орёл-решка). Значит, вероятность этого равна 
.
А, вспомнил метод решения. Это формула комбинаторики «сочетание с повторениями» (не знаю, учили ли её в школе). Берётся не формула размещения потому, что порядок элементов не важен.
у нас равен двум, а 
— трём:
То есть, количество возможных сочетаний равно четырём. Поэтому вероятность одного сочетания (любого, к слову) — 1/4.
