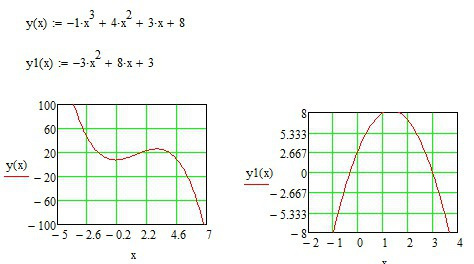
Точки экстремума - это точки, в которых производная y'(x) равна нулю. Уравнение производной y'(x)=-3*x²+8*x+3 - парабола. Равенство производной нулю определяем путём решения квадратного уравнения, в итоге находим координаты x1=-0,333 и x2=3. В точке x1 производная меняет знак с - на + и поэтому эта точка локального максимума, в точке x2 - c + на минус и поэтому это точка локального максимума. График функции и производной y1(x) показаны на рисунке.