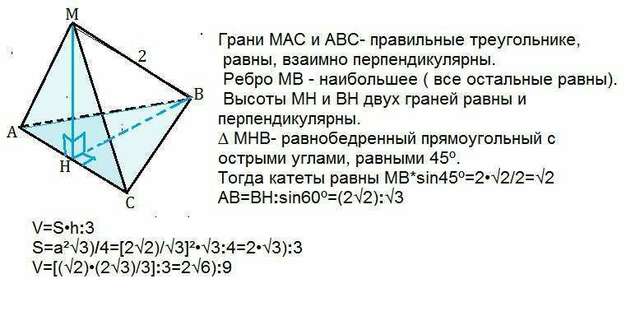
Сделаем и рассмотрим рисунок пирамиды МАВС
Грани МАС и АВС- правильные треугольнике, равны, взаимно перпендикулярны. Ребро МВ - наибольшее ( все остальные равны).
Высоты МН и ВН двух граней равны, перпендикулярны. ∆ МНВ- равнобедренный прямоугольный с острыми углами, равными 45º.
Тогда катеты равны МВ*sin45º=2•√2/2=√2
AB=BH/sin60º=(2√2)/√3
V=S•h/3
S=a²√3)/4=[2√2)/√3]√3/4=2•√3):3
V=[(√2)•(2√3)/3]:3=2√6):9