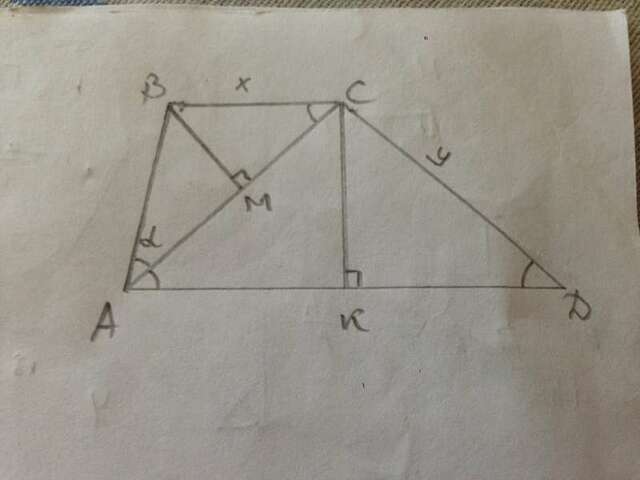
Треугольники АСД и АВС равнобедренные по условию.
∠ВСА=∠САД как накрест лежащие при параллельных АД и ВС и секущей АС, значит углы при основаниях в тр-ках АВС и АСД равны.
ВМ⊥АС, СК⊥АД.
Пусть ∠ВАС=α, ВС=х, АС=у, тогда АМ=у/2, АД=ВС+СД=х+у.
В тр-ке АВМ АМ=АВ·cosα или у/2=х·cosα ⇒ y=2x·cosα.
В тр-ке АСК АК=АС·cosα или (х+у)/2=у·cosα,
(x+2x·cosα)/2=2x·cos²α,
x+2x·cosα=4x·cos²α, x сокращается,
4cos²α-2cosα-1=0, решаем как квадратное уравнение с неизвестным cosα ⇒⇒
cosα₁=(1-√5)/4, -1<х<0 - угол тупой<br>cosα₂=(1+√5)/4,
α=arccos(1+√5)/4=36°.
В трапеции АВСД:
∠А=2α=72°,
∠В=180-∠А=108°,
∠Д=α=36°,
∠С=180-∠Д=144° - это ответ.