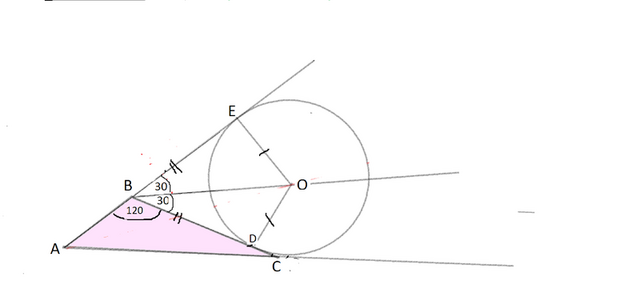
В треугольнике АВС угол В равен 120°, а длина стороны АВ на 3√3 меньше
полупериметра треугольника.
Найдите радиус окружности, касающейся стороны ВС и продолжений сторон АВ и АС.
Сделаем рисунок.
Окружность, радиус которой нужно найти - вневписанная.
Если вневписанная окружность касается стороны ВC треугольника ABC, отрезки касательных от вершины А до точек касания с вневписанной окружностью равны полупериметру треугольника.
Это утверждение вытекает из того, что
по свойству отрезков касательных из точки вне окружности отрезки от В до точек касания равны, равны и отрезки от С до точек касания. Сумма их с соответствующими сторонами треугольника является его полупериметром.
Центр данной окружности лежит на биссектрисе угла СВЕ.
Так как этот угол смежный с углом АВС,
он равен 60°, а угол ОВЕ=30°.
Так как длина стороны АВ на 3√3 меньше полупериметра треугольника, а АЕ - равна полупериметру, то
ВЕ=3√3
Радиус ОЕ:ВЕ= tg (30°) = 1/√3
Радиус ОЕ:ВЕ=R:3√3
R:3√3 = 1/√3
R=3√3 ·1/√3=3