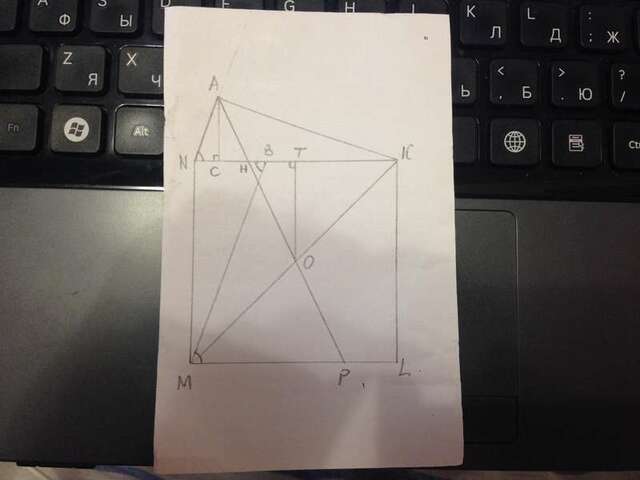
AK=3AN, KB:BN=2:1.
Пусть NB=х, тогда сторона квадрата равна 3х.
а) ∠NBM=∠BML так как NK║ML и МВ - секущая.
В тр-ке MNB tgB=MN/NB=3x/3=3.
В тр-ке AKN tgN=AK/AN=3AN/AN=3.
При параллельных NK и ML ∠ANK=∠BML, значит BM║AN.
Доказано.
б) АР пересекает сторону KN в точке Н. В тр-ках AKN и KOH на сторону KN опустим высоты АС и ОТ соответственно.
Пусть AN=y, AK=3y.
В прямоугольном тр-ке АKN AN²+AK²=KN²,
y²+9y²=9x²,
y=3x/√10.
Высота АС=AN·AK/KN=(3x/√10)·(9x/√10)/(3x)=9x/10.
В тр-ке ACN NC=AC/tgN=3x/10.
CT=NT-NC=(3x/2)-(3x/10)=6x/5.
Треугольники АСН и ОТН подобны (∠АНС=∠ОНТ и оба прямоугольные).
Коэффициент подобия тр-ков АСН и ОТН: k=АС/ОТ=(9х/10):(3х/2)=3/5.
СН/НТ=3/5.
Пусть СН=3z, НТ=5z.
СТ=CH+HT=3z+5z=8z,
8z=6x/5,
z=3x/20.
СН=9х/20, НТ=3х/4.
NH=NC+CH=(3x/10)+(9x/20)=3x/4.
КН=КТ+НТ=(3х/2)+(3х/4)=9х/4.
NH:KH=(3х/4):(9х/4)=1:3.
Треугольники КОН и МОР равны так как ∠НОК=∠РОМ (как вертикальные), ∠ОКН=∠ОМР (KN║ML и КМ - секущая), МО=ОК.
KN=ML, КН=МР, значит LP:PM=NH:KH=1:3 - это ответ.