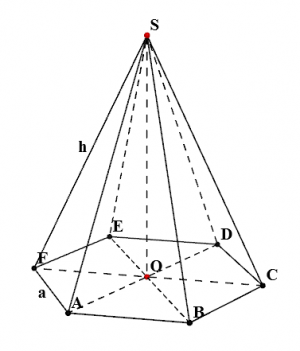
Высота SO=24, боковое ребро SА=25.
Треугольник AOS-прямоугольный, по теореме Пифагора найдем катет АО=SА в квадрате-SО в квадрате все под корнем=25 в квадрате-24 в квадрате все под корнем=7
По свойствам правильного шестиугольника, треугольник AOB является правильными треугольником. Отсюда следует, что АО=ОВ=АВ=7.
В правильной пирамиде все боковые грани равнобедренные треугольники. Треугольник АSВ-равнобедренный.
1. Найдем высоту проведенную к основанию АВ, она будет являться еще и медианой, и соответственно делить основание на 2 равных отрезка оавных 3,5. Высота образует прямоугольный треугольник с катетом 3,5 и гипотенузой 25. По теореме Пифагора найдем высоту=25 в квадрате-3,5 в квадрате все под корнем=612,75 под корнем
2. Площадь треугольника=0,5 основание*высоту или 0,5* сторону* высоту к стороне
Площадь=0,5*7*612,75 под корнем=3,5*(612,75 под корнем)
Тогда высота к боковой стороне=2*площадь/сторону=2*3,5*(612,75 под корнем)/25 =0,28 (612,75 под корнем)