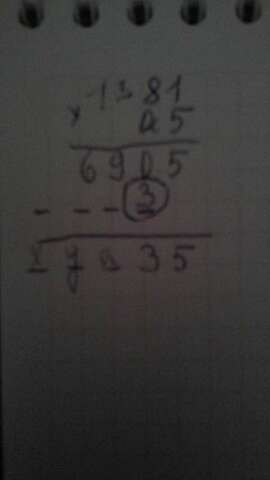Найдите произведение двух двузначных чисел, о которых известно следующее: если к первому...

Question

Найдите произведение двух двузначных чисел, о которых известно следующее: если к первому числу приписать справа второе число, а затем цифру 0, то
получиться пятизначное число,который при делении на второе заданное число дает в частном 1381 и в остатке 15. если к первому заданному приписать справа второе число а затем составить новое четырехзначное число которое получиться приписыванием к первому числу второго слева, то первое четырехзначное число окажется больше второго четырехзначного числа на 1287?
Заранее спасибо)
Ответ должен получиться 1680, но у меня не получается!

Answer 1

Ху*ав - ?
ху и ав - двузначные числа. разные буквы, разные цифры.

хуав0:ав=1381 (ост15)
хуав-авху=1287

1381*ав+15=хуав0
в=5, т.к. при сложении с 15 последняя цифра должна быть 0, а 5*1=5 и 5+5=10.
1381*а5+15=хуа50
=> 1381*а5=хуа35 (50-15=35)
если произвести умножение в столбик (см. фото), получим, что а=3.
=> 1381*35=48335
=> х=4, у=8
=> ху=48, ав=35
проверим:
хуав-авху=1287
4835-3548=1287, все верно.
=>
48*35=1680

---