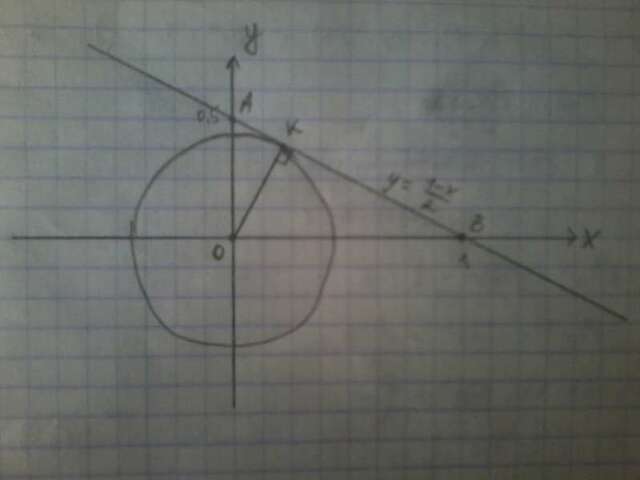
Обычно задания такого типа довольно просто решаются графически.
Заметим, что первое уравнение в системе - уравнение окружности с центром в точке (0;0), где а - радиус окружности в квадрате, а второе уравнение - линейная функция, которую нужно всего лишь немного преобразовать.
x+2y=1
y=(1-x)/2 или y=0.5-0.5x
Сделаем чертёж и обозначим точки пересечения прямой с осями буквами А и В. Точка (0;0) - буква О.
Система имеет одно решение, только когда линейная функция касается этой окружности. Если радиус окружности уменьшать, то решений (пересечений) вовсе и не будет. Если увеличивать, то будет всегда 2 решения.
Заметим, что радиус окружности, проведённый в точку касания - перпендикуляр к касательной. То есть нам осталось всего лишь найти длину высоты ОК в треугольнике, образованном осями координат и касательной к окружности, и возвести её в квадрат.
Найдём гипотенузу АВ: 
S(ΔAOB) = (0.5*1)/2 = 0.25
S(ΔAOB) = OK*AB/2, откуда OK = 2*S(ΔAOB)/AB = 1/√5
a = OK² = 1/5
Ответ: 1/5.