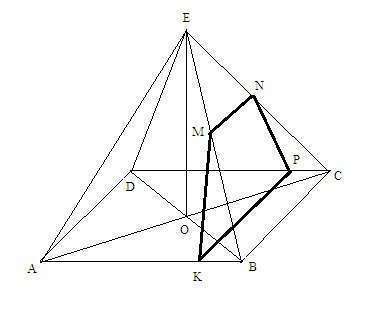
В основании пирамиды квадрат с диагональю
AC = BD = d = 16√2.
AO = BO = CO = DO = d/2 = 8√2
Значит, сторона квадрата
AB = BC = CD = D = a = 16
Боковая сторона
AE = BE = CE = DE = L = 18
Высота пирамиды
OE = H = √(AE^2-AO^2) = √(18^2-64*2) = √(324-128) = √196 = 14
Сечение KMNP - это равнобочная трапеция
KP || BC, KP = 16
MN - средняя линия тр-ника BCE, MN = 8
Высота трапеции h = H/2 = 7
Площадь S(KMNP) = (KP + MN)*h/2 = (16 + 8)*7/2 = 84 кв.см.