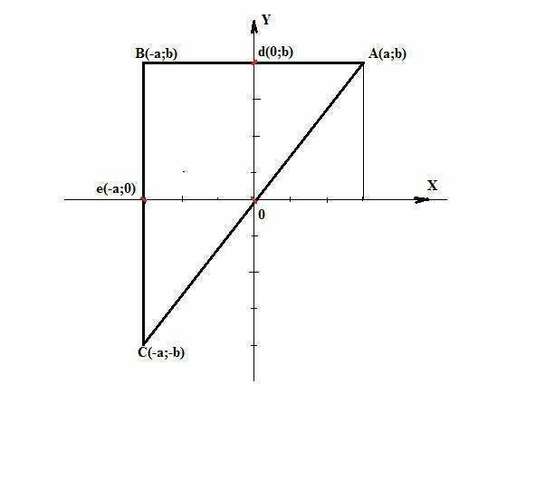
У точек А и В координата y одна и та же. Следовательно, сторона АВ параллельна оси Х и пересекает ось Y в точке d(0;b).
У точек B и C координата x одна и та же. Следовательно, сторона ВC параллельна оси Y и пересекает ось X в точке e(-a;0).
Или так:
Уравнение прямой, проходящей через две точки:
(х-х1)/(х2-х1)=(y-y1)/(y2-y1).
Прямая АВ: (х-a )/((-a)-a)=(y-b)/(b-b) или (x-a)/-2a=(y-b)/0.
Или 0*(X-a)=-2a*(y-b) или -2a*(y-b)=0.
Отсюда уравнение прямой АВ: y=b.
Следовательно, сторона АВ параллельна оси Х и пересекает
ось Y в точке d(0;b).
Прямая ВC: (х+a )/((-a)-(-a))=(y-b)/(-b-b) или (x-a)/0=(y-b)/2b.
Или 2b*(X-a)=0*(y-b) или 2b*(X-a)=0.
Отсюда уравнение прямой ВC: x=-a.
Следовательно, сторона ВC параллельна оси Y и пересекает
ось X в точке e(-a;0).
Прямая AC: (х-a )/((-a)-a))=(y-b)/(-b-(-b)) или (x-a)/-2a=(y-b)/-2b.
Или 2b*(x-a)=2a*(y-b) или b*(x-a)=a*(y-b).
Уравнение оси абсцисс y=0, оси ординат х=0.
Тогда пересечение стороны АС с осью Х (y=0):
bx-ba=-ba или х-а=-а или х=0.
Пересечение стороны АС с осью Y (х=0):
-ba=-ay-ba или y-b=-b или y=0.
То есть координаты пересечения прямой АС с осями ординат: Х=0 и Y=0 (начало координат).
Ответ: пересечение сторон треугольника с осями ординат
в точках с координатами d(0;b), e(-a;0) и o(0;0).