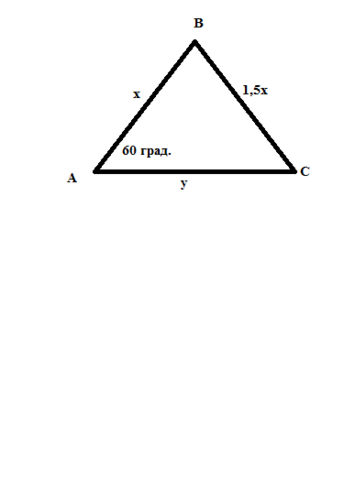
Здесь лучше использовать теорему косинусов:  0." alt="(1,5x)^{2}=x^{2}+y^{2}-2xycos60\\2,25x^{2}-x^{2}-y^{2}-xy=0|:x^{2}\\2,25-1-(\frac{y}{x})^{2}-\frac{y}{x}=0\\\frac{y}{x}=t\\t^{2}+t-1,25=0\\D=1+5=6\\t_{1}=\frac{-1-\sqrt{6}}{2};t_{2}=\frac{-1+\sqrt{6}}{2}\\\frac{y}{x}=\frac{-1-\sqrt{6}}{2};\frac{y}{x}=\frac{-1+\sqrt{6}}{2}\\\frac{y}{1,5x}=\frac{-1-\sqrt{6}}{3}<0;\frac{y}{1,5x}=\frac{-1+\sqrt{6}}{3}>0." align="absmiddle" class="latex-formula">
0." alt="(1,5x)^{2}=x^{2}+y^{2}-2xycos60\\2,25x^{2}-x^{2}-y^{2}-xy=0|:x^{2}\\2,25-1-(\frac{y}{x})^{2}-\frac{y}{x}=0\\\frac{y}{x}=t\\t^{2}+t-1,25=0\\D=1+5=6\\t_{1}=\frac{-1-\sqrt{6}}{2};t_{2}=\frac{-1+\sqrt{6}}{2}\\\frac{y}{x}=\frac{-1-\sqrt{6}}{2};\frac{y}{x}=\frac{-1+\sqrt{6}}{2}\\\frac{y}{1,5x}=\frac{-1-\sqrt{6}}{3}<0;\frac{y}{1,5x}=\frac{-1+\sqrt{6}}{3}>0." align="absmiddle" class="latex-formula">
Последние два равенства есть отношение АС к ВС, но первое меньше нуля, следовательно не может быть такого.
Ответ: