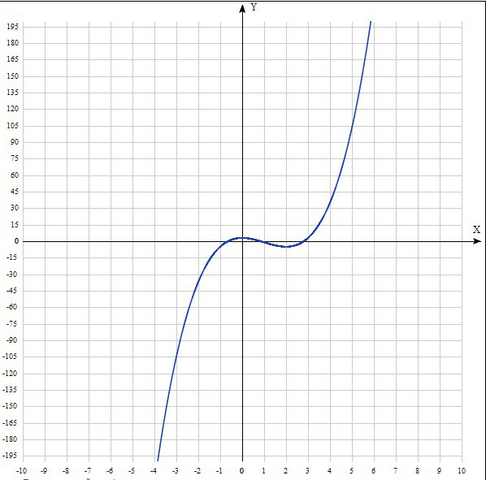
1. Область определения: определена на всей числовой прямой т.е. х∈ (-∞;+∞)
2. Асимтоты отсутствуют
3. Функция является нечетная, так-как не выполняется условие f(x)=f(-x)
4. Промежутки возрастания и убывания
f'(x)≥0 и f'(x)≤0
f'(x)=6x²-12x
6x²-12x≥0
6x²-12x=0 ⇒ x1=0 x2=2.
Функция возрастает на промежутке (-∞;0] и [2;+∞) и убывает на промежутке (0;2)
5. Промежутки выпуклости и вогнутости
f''(x)≥0 и f''(x)≤0
f''(x)=12x-12
x=1. это точка перегиба, до нее функция выпуклая, после нее вогнутая.