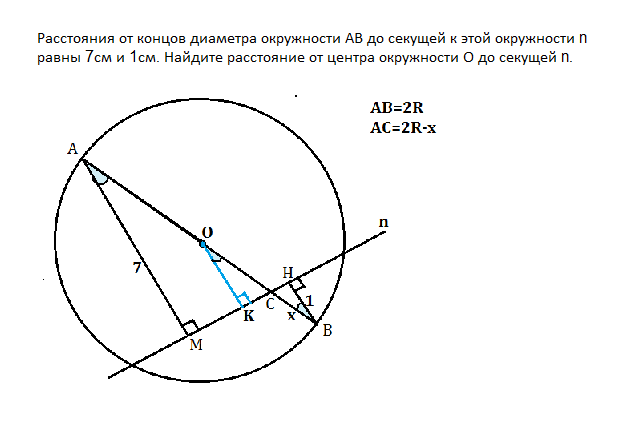
Обозначим точку пересечения диаметра и секущей буквой С.
Расстояние от точки до прямой измеряется длиной перпендикулярного к ней отрезка.
Обозначим основание отрезка из А буквой М, из В - Н.
AO=R, АВ=2R
Пусть ВС=х
Тогда АС= 2 R-x,
Так как треугольники АМС и ВНС прямоугольные, АМ || ВН как два перпендикуляра к одной прямой, а диаметр - секущая между двумя параллельными прямыми.
Тогда углы А и В равны как накрестлежащие.
∆ АМС~∆ ВНС по двум равным углам
АМ:ВН=АС:ВС
7:1=(2R-x):x
7х=2R-x
2R=8x
R=4x
Тогда ОС=4х-х=3х
Расстояние от центра окружности до прямой n - перпендикуляр ОК.
∆ ОКС~∆ ВНС
ОС:ВС=ОК:ВН
3:1=ОК:1 ⇒
ОК=3 см