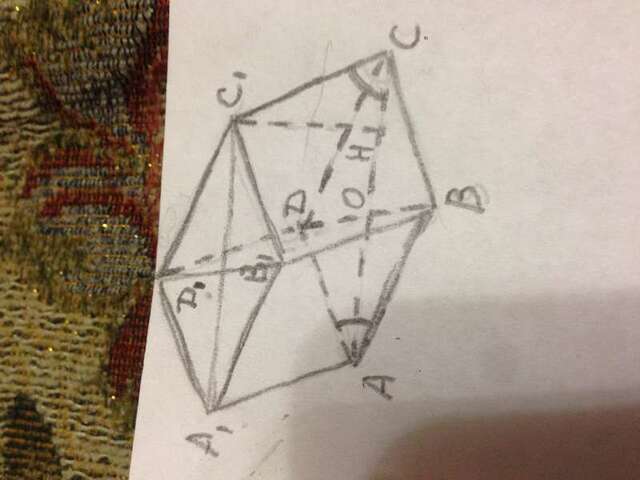
Сечения ВВ1Д1Д и АА1С1С перпендикулярны , так как в основании призмы ромб, а в нём ВД⊥АС.
ВВ1Д1Д - прямоугольник, АА1С1С - параллелограмм с острым углом АСС1=60°.
Пусть сторона основания равна х, а боковое ребро равно у.
Площадь прямоугольника ВВ1Д1Д: S1=ВД·ВВ1.
В тр-ке АВД АВ=ВД, ∠ВАД=60°, значит он равнобедренный, в котором углы при основании равны 60 и 60°, значит он правильный, ВД=АВ=х. АО=АВ·sin60=x√3/2.
S1=х·у.
В параллелограмме АА1С1С опустим высоту С1Н на сторону АС.
В тр-ке СС1Н С1Н=СС1·sin60=y√3/2.
Площадь АА1С1С: S2=АС·С1Н, AC=2AO=x√3.
S2=х√3·у√3/2=3ху/2.
Отношение площадей ВВ1Д1Д и АА1С1С:
S1/S2=2ху/3ху=2/3=2:3.
Доказано.