1.

- нет вертикальных асимптот

Функция ни четная, ни нечетная
2.

нет наклонных асимптот

идем вправо - уходим далеко вниз
идем влево - уходим далеко вверх

3.

Точки пересечения с осями
4.


__-__0__+__

убывает

возрастает

точка минимума

точка максимума
5.

__+__1__-__

вогнутая

выпуклая

точка перегиба
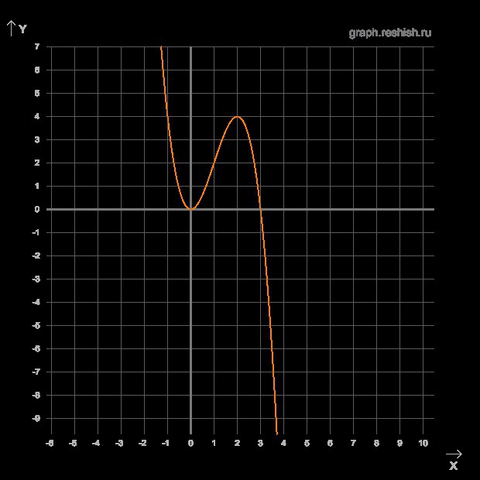
График прилагается