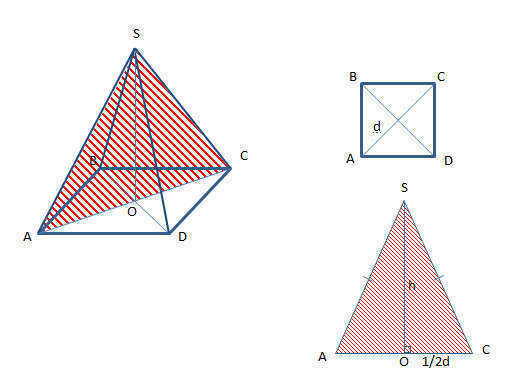
У меня получилось так:
S осн=1/2*d1*d2, тк d1=d2, то Sосн=d^2/2
S сеч=1/2*AC*SO=1/2*d*h
Из условия: 2*Sосн=Sсеч, тогда
2*d^2/2=1/2*d*h, тогда h=2*d
Боковая сторона сечения (по т.Пифагора)SC^2 =(2*d)^2+(1/2*d)^2/
SC=d/2*√17
Из тр. SOC:
CosCSH=(2*h):(d/2*√17)=4/√17
SinCSH=(d/2):(d/2*√17)=1/√17
Угол при вершине=2*CSH
Cos двойного угла: cos(2α) = cos²(α) - sin²(α)
Искомый Cos=(4/√17)^2-(1/√17)^2=15/17