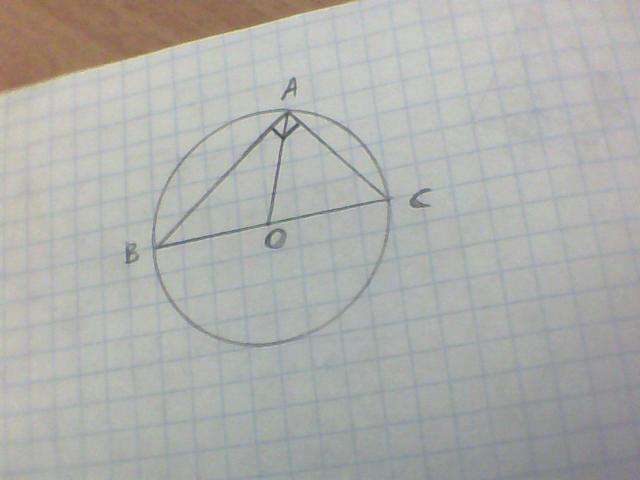1.В прямоугольном треугольнике гипотенуза равна 60 см.Найди медиану,проведенную к...

Question

1.В прямоугольном треугольнике гипотенуза равна 60 см.Найди медиану,проведенную к гипотенузе. (Ребят,чертеж нужен обязательно и решение,чертеж напишите и сфоткайте на листе) 2.Это по желанию,кто сделает дарю +15 пкт. бесплатно.Вот:Биссектриса прямоугольного угла образует с гипотенузой угол,равный 65 градусов.Найти все угы в треугольнике.

Answer 1

1) В прямоугольном треугольнике центр описанной окружности лежит на середине

     гипотенузы, значит ОВ=ОС=ОА=R

     Медиана АО=1/2ВС=30 см

 

 

2) Биссектриса делит прямой угол прямоугольного треугольника на 2 угла по 45⁰

     Значит:

    Один острый угол прямоугольного треугольника равен 180-(65+45)=70⁰

    Второй острый угол прямоугольного треугольника равен 180-(90+70)=20⁰

Answer 2

1. Вокруг любого треугольника можно описать окружность. Если описать окружность вокруг прямоугольного треугольника, то ее центр будет лежать на середине гипотенузы, а сама гипотенуза будет диаметром этой окружности. Медиана - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Вершина A лежит на окружности, середина противолежащей стороны BC - точка О, центр окружности. Значит медиана AO - радиус описанной окружности. D = 60 см отсюда R = 30 см.

 

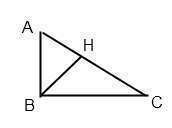
2. Биссектриса делит угол ABC на два равных угла по 45°, угол AHB = 65° ( по условию ), значит угол BAC = 180 - ( 45 + 65 ) = 70°.

Угол BCA = 180 - ( 90 + 70 ) = 20°.

 

---

---