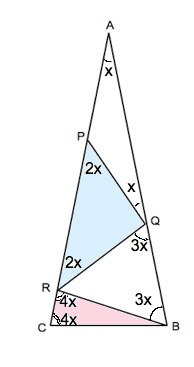
Треугольник АВС - равнобедренный. Примем ∠А= х.
Треугольник АРQ - равнобедренный, ∠AQP=∠QAP=x.
∠ RPQ – внешний угол ∆ APQ при вершине Р и р (свойство).
∠RPQ=2х.
Угол RQB внешнийпри вершине Q треугольника RAQ.
∠RQB=∠А+∠PRQ=x+2x=3x.
Угол BRC - внешний при вершине R треугольника BRA.
∠BRC=угол А+угол АВR=3х, и, наконец,
∠BRC=4х.
В равнобедренном треугольнике BRC угол С=4х, в равнобедренном
∆ АВС угол В=4х, и тогда
4х+4х+х=180°, откуда х=20° ⇒ ∠А=20°