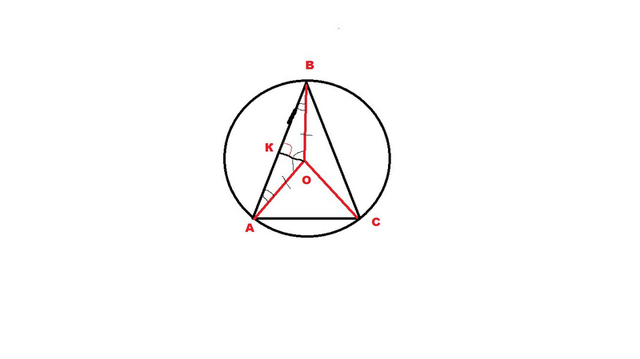
Дано:
Δ АВС
∠ АОВ = 120°
АВ=20
АС и ВС - серединный перпендикуляр
___________
Найти: ОС
Решение:
ОС - радиус описанной окружности
Рассмотрим Δ АОВ
АО = ВО = СО - радиус
Значит, Δ АОВ - равнобедренный
Опустим высоту ОК на сторону АВ
ОK ⊥ АВ и является еще биссектрисой и медианой по свойству равнобедренного треугольника
Δ ВОК - прямоугольный
∠К = 90°
∠О = 120:2 = 60°
∠В = 180-90-60 = 30°
ВК = 20:2=10
ОВ = х
ОК = х:2 (как сторона лежащая против угла в 30° равна половине гипотенузы)
По теореме Пифагора находим ОВ(помним, что ОВ=ОС=ОА):